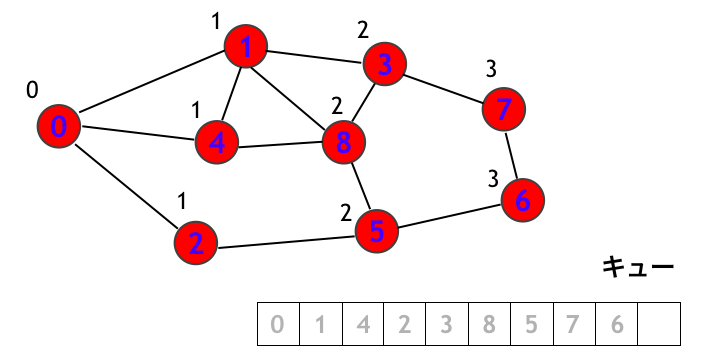
from collections import deque
def bfs(root, target):
    step = 0
    # Enqueue root node in queue
    q = deque([root])
    # Set to store visited nodes
    visited = set(q)

    while q:
        size = len(q)
        # Iterated the nodes which are already in the queue
        for _ in range(size):
            # Pop the first node in the queue
            curr = q.popleft
            if curr == target: return step
            # Search all adjacent nodes of current node and append them to queue
            for neighbor in (the adjacent nodes of curr):
                # Skip if we already visited the node
                if neighbor in visited continue:

                q.append(neighbor)
                visited.add(neighbor)
        # Increment step for each search of the node
        step+=1

    # Return -1 if there is no target node
    return -1

# Recursion
def dfs(self, curr: int, target: int, visited: Set[int]):
    # Base case
    return True if curr == target
    for next_node in (each neighbor of curr):
        if next_node is not in visited:
            visited.add(next_node)
            self.dfs(next_node, target, visited)
    return False

# Iteration
def dfs(self, root: int, target: int) {
    visited = set()
    stack = [root]
    while stack:
        cur = stack.pop()
        return True if cur == target
        for next in (the neighbors of cur):
            if next is not in visited:
                visited.add(next)
                stack.append(next)

    return False
}