Binary Tree

DSA
Page content

Overview

A tree is a frequently-used data structure to simulate a hierarchical tree structure.

Each node of the tree will have a root value and a list of References to other nodes that are called child nodes. From graph view, a tree can also be defined as a directed acyclic graph that has N nodes and N-1 edges.

A Binary Tree is one of the most typical tree structures. As the name suggests, a binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.

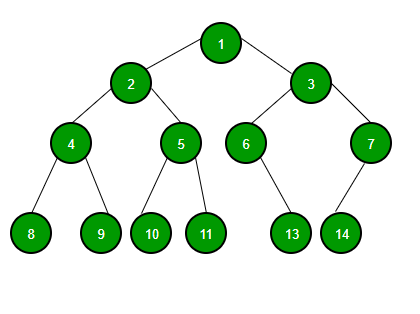
binary tree

A Binary Tree node contains the following parts.

Data Pointer to a left child Pointer to a right child

# Definition for a binary tree node.
class TreeNode:
	def __init__( val=0, left=None, right=None):
		val = val
		left = left
		right = right

Types of binary tree

There are many types of binary tree

Full Binary Tree

All nodes except leaf nodes have two children.

Full Binary tree

Complete Binary Tree

All the levels are completely filled except possibly the last level and the last level has all keys as left as possible.

Complete Binary tree

Perfect Binary Tree

All the internal nodes have two children and the all leaf nodes are at the same level.

Perfect Binary tree

Balanced Binary Tree

The height of the tree is O(Log n) where n is the number of nodes.

A degenerate (or pathological) tree

Every internal node has only one child.

Pathological tree

Depth First Traversals

DFS

Implementation

from binarytree import tree
from binary_tree import TreeNode
from typing import List

# recursive solution
def traverse(root: TreeNode) -> List[int]:
    ans = []
    traverse(root, ans)
    return ans

def inorder_traverse(root: TreeNode, ans: List[int]):
    if root:
        traverse(root.left, ans)
        ans.append(root.val)
        traverse(root.right, ans)

def preorder_travese(root: TreeNode, ans: List[int]):
    if root:
        ans.append(root.val)
        traverse(root.left, ans)
        traverse(root.right, ans)

def postorder_travese(root: TreeNode, ans: List[int]):
    if root:
        traverse(root.left, ans)
        traverse(root.right, ans)
        ans.append(root.val)

“Breadth First Traversals”:

Level order traversal of a tree is breadth first traversal for the tree.

1 2 3 4 5

# Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
from itertools import chain
def levelOrder(root: TreeNode) -> List[List[int]]:
    if not root:
        return []
    ans, same_lev = [], [root]
    while (same_lev):
        ans.append((map(lambda node: node.val, same_lev)))
        tmp = chain.from_iterable(map(lambda node: [node.left, node.right], same_lev))
        same_lev = [leaf for leaf in tmp if leaf]
    return ans


from binary_tree import TreeNode
from typing import List
import queue

# Implementation using queue
def bfs(root: TreeNode) -> List[int]:
    ans = []
    my_queue = queue.Queue()
    my_queue.put(root)

    while not my_queue.empty():
        root = my_queue.get()
        ans.append(root.val)

        if root.left:
            my_queue.put(root.left)

        if root.right:
            my_queue.put(root.right)
    return ans

References

Binary Tree Data Structure

Introduction to Data Structure Binary Tree

[Binary Tree | Set 3 (Types of Binary Tree](<https://www.geeksforgeeks.org/binary-tree-set-3-types-of-binary-tree/)